Next: TP 2 : Programmation Up: Previous: Contents Contents

Subsections

TP 1 : Prise en Main de Matlab

Ce TP a pour but d'apprendre à utiliser le logiciel Matlab, et de manipuler les variables dans l'environnement de travail. Les différents types de visualisation des données en 2D et 3D sont aussi abordés. Enfin l'utilisation de scripts et de fonctions est présentée au travers d'exemples simples.

Compte rendu du TP

Ce TP est réparti sur les 2 premières séances. La première séance ne proposant que peu d'applications, le travail demandé est d'expliquer les fonctions utilisées mais aussi de noter toutes les erreurs que vous rencontrerez et de les expliquer.

Lorsqu'une erreur se produit, un commentaire visant à l'expliquer s'affiche dans l'espace de travail. Il est conseillé de bien lire ce commentaire pour comprendre et cerner l'erreur.

Un certain nombre d'erreurs sont assez fréquentes et il est donc indispensable de savoir d'où elles viennent pour les corriger facilement.

$\fbox{\parbox{\textwidth}{\centerline{{\bf Ne notez qu'une seule fois le même type d'erreur !}}}}$

Génération - Manipulation

Cette partie fait un tour d'horizon des utilisations courantes des vecteurs et matrices, de la génération à l'indexation.

On travaille dans cette partie à partir du prompt de l'espace de travail. Le prompt, dénoté par >>, signifie que vous avez la main et qu'une commande est attendue.

Quelques commandes sont utiles, lorsque vous avez oublié quelles sont vos variables ou une commande ...

Les commandes who et whos vous indiquent les tailles et types de vos variables.
La commande help utilisée seule donne une liste et un bref descriptif des sujets contenant une aide,
La commande help nom_fonction donne un descriptif de la fonction sur les arguments nécessaires en entrée ainsi que les résultats donnés.

Manipulations des vecteurs et scalaires

Scalaires

Dans un premier temps on génére trois variables scalaires a,b et c sur lesquelles on va par la suite effectuer quelques opérations.

>> a = 2
a =
     2
>> b = 3
b =
     3
>> c = 4;
>>

Le caractère `;' sert à supprimer l'écho d'une ligne de commande, c'est-à-dire l'affichage des valeurs prises par les variables dans la ligne de commande. Pour connaître la valeur d'une variable, il suffit donc de taper son nom :

>> c
c =
     4

Il est aussi possible de séparer 2 commandes sur la même ligne à l'aide d'une virgule `,' sans supprimer l'écho ou d'un point virgule `;'. Essayez :

>> a = 3; b = 2, c = 4;

Enfin, si une ligne de commande est trop longue, vous pouvez passez à la ligne suivante en tapant `...' puis $\fbox{{\em Entrée}}$ :

>> a = ...
4
a =
     4

Vous pouvez alors effectuer des opérations sur vos variables en respectant les règles classiques de priorités : * et / prioritaires devant + et -

>> a+b * c  
ans =
    16
>> (a+b) * c
ans =
    28
>> d = a/b*c, e = (a/b)*c
d =
     6
e =
     6

Comparez alors l'effet des commandes who et whos.

Vecteurs

Les vecteurs peuvent être générés de manière manuelle ou automatique. Pour la génération manuelle, les délimiteurs sont :

`[' et `]' délimitent le début et la fin du vecteur,
un espace sépare 2 colonnes,
un point virgule `;' à l'intérieur de [ ] sépare 2 lignes.

Générez ainsi un vecteur ligne et un vecteur colonne

>> vect1 = [ a b c+b/2 ] 
  ???
>> vect2 = [ c; b; a+b+c] 
  ???

La transposition s'effectue à l'aide de l'apostrophe '. Attention, car elle effectue aussi l'opération de conjugaison si le nombre est complexe (c'est la transconjugaison), et la transposition réelle est en fait l'opérateur .'. Essayer

>> vect1 + vect2
  ???
>> vect1 + vect2'
  ???
>> (vect2 + i)'
  ???
>> (vect2 + i).'
  ???

La génération automatique d'un vecteur se fait de manière linéaire ou logarithmique. De manière linéaire, en définissant une valeur de début, un pas et une valeur de fin, chacuns séparés par 2 points ` :'. Par défaut, c'est à dire s'il n'est pas spécifié, le pas vaut 1. Essayez :

>> vect3 = 1:10 
   ???
>> vect4 = 1:-0.5:-1
   ???
>> debut = 0; fin = 2*pi; pas = .1; vect5 = debut:pas:fin

Essayez alors les fonctions linspace et logspace pour générer des vecteurs linéaires ou logarithmique (regardez l'aide sur ces fonctions pour savoir comment les utiliser).

Les opérations +,-,*,^ sur les vecteurs se font alors comme pour les matrices et il est en plus possible de faire des opérations terme à terme en ajoutant un point devant l'opérateur (.* , ./ ,.^ , ...). Les principales règles sont rappelées

L'addition/soustraction de matrices est possible si et seulement si les matrices sont de même taille.
La multiplication de deux matrices est possible si et seulement si ces matrices ont une taille en commun. $A_{(N_1,M_1)}*B_{(N_2,M_2)}$ existe si . Le produit est alors effectué dans l'ordre classique ligne - colonne
La puissance n'a de sens que pour les matrices carrées.
Les opérations terme à terme ne sont possibles qu'entre des matrices de même taille.
La puissance et l'inverse terme à terme sont possibles sur toutes les matrices (pour l'inverse, il ne doit pas y avoir d'éléments nuls).

L'utilisation des fonctions mathématiques courantes se fait comme dans une calculatrice scientifique. Une liste des fonctions les plus courantes est disponible dans l'aide en ligne par
>>help elfun
Essayez et commentez les opérations suivantes

>> vect1 * vect2 
>> vect2 * vect1 
>> vect1 .* vect2' 

>> x = 0:pi/4:pi;
>> sin(x),cos(x), 1/x        
   ???

Manipulations des matrices

Les matrices sont des tableaux à deux dimensions qui se génèrent comme les vecteurs. À l'intérieur des délimiteurs [ ], deux colonnes sont séparées par un espace et deux lignes par un point virgule `;'.
Surveillez bien que toutes vos lignes aient toujours le même nombre de colonnes !
Un certain nombre de matrices prédéfinies existent (diagonales, nulles, remplies de 1, ...), et fonctions réalisent les opérations courantes sur les matrices (déterminant, trace, somme des lignes ou des colonnes, valeurs propres, ...). La liste est disponible dans l'aide :

>> help elmat

Générez la matrice $A_{(3,3)}$ donnée ci-dessous, recherchez son déterminant, son inverse, son carré, son inverse terme à terme. Vérifiez que $A * A^{-1} = I_{(3,3)}$ .

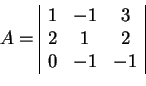
$\begin{displaymath}A = \begin{array}{\vert ccc\vert} 1 & -1 & 3 \\ 2 & 1 & 2 \\ 0 & -1 & -1 \end{array} \end{displaymath}$

Exemple de résolution de système linéaire

Il est facile de résoudre un système linéaire sous Matlab, grace aux fonctions divisions \ et /, respectivement dites à gauche et à droite. Il faut pour comprendre cela, rappeler un résultat essentiel de la multiplication de 2 matrices :

$\fbox{\parbox{\textwidth}{\centerline{Le produit de 2 matrices n'est pas commutatif !}}}$

Pour vous en convaincre, générez une matrice et comparez les résultats des multiplications et .

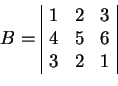
$\begin{displaymath}B = \begin{array}{\vert ccc\vert} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 3 & 2 & 1 \end{array} \end{displaymath}$

L'écriture sous forme de produit matriciel d'un système d'équations linéaire respecte un certain ordre dans la multiplication. Ainsi le système :

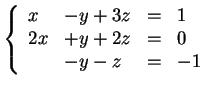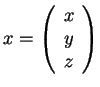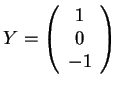$\displaystyle \left\lbrace \begin{array}{llll} x & - y +3z & = & 1 2x & + y + 2z & = & 0 & -y -z & = & -1 \end{array} \right.$ s'écrit : $\displaystyle A*x = Y$ , où $\displaystyle x = \left( \begin{array}{c} x y z \end{array} \right)$ et $\displaystyle Y = \left( \begin{array}{c} 1 0 -1 \end{array} \right)$

(1.1)

Dans ce cas là on a recours à la division à gauche car la matrice

est située à gauche de l'inconnu. La solution du système sera donnée par $x = A \backslash Y$ , comme pour signifier que

divise

par la gauche. La division à droite est utilisée dans un système du type

.
Résolvez le système proposé sous Matlab.

Indexation des matrices

Les manipulations fréquentes sur les matrices nécessitent souvent de ne récupérer qu'une partie d'une matrice (ligne ou colonne, sous matrice). L'indexation, ou appel des éléments se fait par rapport à leurs indices, numérotés de 1 au nombre total de ligne puis de 1 au nombre total de colonnes. L'ordre d'indexation est toujours ligne - colonne.
Pour récupérer l'élément situé à la ligne, colonne de la matrice A, on appelle . Récupérer ainsi l'élément 0 dans la matrice A.

>> a(2,3)
ans =
     2

Afin de récupérer un sous bloc d'une matrice, il faut donner en indice non plus une valeur mais un vecteur de valeur. La récupération d'une ligne ou d'une colonne se fait en indiquant `:' comme indice. Le dernier élément d'une ligne ou d'une colone peut être indexé par la variable end.
Essayez et commentez

>> a(1:2,1)
>> a(1,:)  
>> a(:,1:3)
>> a(1:2,2:3)
>> a(end,end-1)

Dans le cas où l'on ne veut récupérer que quelques éléments de la matrice, il faut avoir recours à un autre type d'indexation. Matlab indexe en effet les éléments de 2 façons : soit en ligne - colonne, soit comme un vecteur, en comptant les éléments dans l'ordre ligne colonne.
Pour la matrice

, les éléments sont donc soit indexés de

, soit de

dans l'ordre :

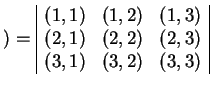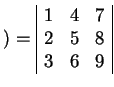$\displaystyle ($ lignes,colonnes $\displaystyle ) = \begin{array}{\vert ccc\vert} (1,1) & (1,2) & (1,3) (2,1) & (2 ,2) & (2,3) (3,1) & (3 ,2) & (3,3) \end{array}$ , soit $\displaystyle ($ indices $\displaystyle ) = \begin{array}{\vert ccc\vert} 1 & 4 & 7 2 & 5 & 8 3 & 6 & 9 \end{array}$

(1.2)

La conversion (ligne,colonne) vers (indice) se fait alors, pour une matrice ayant

lignes et

colonnes :

indice $\displaystyle = N*($ colonne $\displaystyle -1) + ligne$

Essayez avec les 2 types d'indexations de récuperer en une seule fois les éléments

. Concluez.

Suppression d'éléments, taille des matrices

Il est parfois utile de devoir supprimer, ou ajouter, des éléments d'un vecteur ou d'une matrice. L'ajout d'éléments se fait simplement en assignant une valeur à l'indice désiré. Matlab met à jour la taille des matrices pour y inclure le nouvel élément.
La taille des matrices est donnée par la fonction size pour les matrices ou les tableaux de dimensions et par length pour les vecteurs. Une option intéressante de la fonction size est la possibilité de ne récupérer que le nombre de lignes ou de colonnes d'une matrice.
Regardez dans l'aide de la fonction size.
Essayez et commentez les ajouts suivants. Vérifiez aussi la taille de votre matrice avant et après chacune des opérations.

>> a(5,2) = 5
>> a(4,:) = 5
>> a(1:4,7) = a(1,3)

L'opération de concaténation consiste à mettre bout à bout des matrices, ou vecteur. Il n'est possible de concaténer les matrices en ligne ou en colonne que si elles ont une dimension en commun.
Expliquez les concaténations suivantes :

>> aa1 = [ a a ]
>> aa2 = [ a ; a ]
>> aa3 = [ a(1,:) ; a(:,2)' ]
>> aa4 = [ a(1,1:2) , a(1:2,4) ]

Il est aussi nécessaire, pour certaines opérations terme à terme entre 2 matrices de répliquer un vecteur ou une matrice pour le mettre au format d'une autre. La commande repmat permet de répliquer une matrice en la concaténant.
Expliquez chaque terme des commandes suivantes

>> c = repmat(1:size(a,2),size(a,1),1)     
>> d = a.^c

Enfin, pour supprimer des éléments d'une matrice, il faut en fait leur assigner une matrice vide (>> [ ]).
Est-il possible de ne supprimer qu'un élément d'une matrice ?
Commentez les opérations suivantes, en vérifiant la taille de votre matrice

>> a(4,:) = [ ]
>> a(5,:) = [ ]
>> a(:,4:6) = [ ]

Utilisation de fichiers scripts

Plutôt que de retaper toute une série de commandes au clavier, le travail sur une application précise en Maltab se fera en créant dans l'éditeur de texte des fichiers textes stockés avec l'extension `` .m''. Tous les fichiers ayant l'extension .m sont exécutables directement depuis le prompt, en tapant le nom du fichier, sans l'extension. Il faut toutefois s'assurer que le chemin du répertoire dans lequel se trouve vos fichiers est bien connu par Matlab. C'est la commande path qui vous indique quels sont les chemins connus. Cette commande permet aussi d'ajouter un chemin à la liste. Les versions récentes de matlab sont équipées d'un path browser (explorateur de chemin) qui vous permet d'ajouter facilement les chemins des répertoires contenant vos fichiers. Il existe 2 types de fichiers .m, les fichiers de commandes et les fichiers de fonctions. Les fonctions seront vues plus tard et nous ne presentons ici que les fichers de commandes.

Les fichiers de commandes sont des fichiers textes, éditables avec n'importe quel éditeur (Notepad, ...). Les versions récentes de Matlab proposent un éditeur de fichiers ``.m'' présentant quelques avantages : couleurs spécifiques pour les fonctions connus, outils de debbugage intégrés, ajout de points d'arrêts, ...
Pour ouvrir un fichier ``.m'' dans l'éditeur, tapez >> edit nom_fichier.

Vous travaillerez désormais uniquement dans des fichiers scripts, afin de garder une trace de vos travaux, et de pouvoir apporter facilement des modifications.

Il est utile de commenter abondamment ces programmes, pour les comprendre facilement même longtemps après leur création. Une ligne de commentaires est délimitée sous Matlab par le caractère ``%''.

$\fbox{\parbox{\textwidth}{\centerline{Un programme sans commentaire, même s'il marche, est un mauvais programme !}}}$

À titre d'exemple, créez un fichier ``.m'' qui génère un signal sinusoïdal de 128 points, puis qui l'affiche à l'écran, à l'aide de la commande plot.
Éxecutez votre programme depuis l'espace de travail (vérifiez que le chemin d'accès au programme existe).

Un autre avantage des scripts est la possibilité de demander une valeur à l'utilisateur pendant l'éxecution du programme. Ceci se fait par la commande input.

>> valeur = input('Entrez une valeur')

Modifiez votre programme pour demander la fréquence du sinus à l'utilisateur.

Affichage

Matlab possède de nombreuses fonctions permettant de visualiser les données que ce soit en 2D, 3D ou même 4D puisqu'il est possible de réaliser des animations (pour voir les vibrations d'une plaque par exemple). Avant tout, il est souvent nécessaire d'afficher du texte, pour demander des valeurs à l'utilisateur ou simplement pour afficher des résultats.

Texte

Il existe 2 grands types de variables : les nombres, souvent réels (double), et les caractères. Dans les 2 cas, Matlab traite les données sous forme matricielle, c'est à dire soit comme un tableau de nombres, soit comme un tableau de caractères. Par exemple, une phrase sans saut de ligne sera un vecteur de caractères.
Les chaînes de caractères sont délimitées par des apostrophes '.

>> txt1 = 'Bonjour les amis'
txt1 =
Bonjour les amis
>> txt1(1:8)
ans =
Bonjour

Pour récupérer une chaîne entrée par l'utilisateur, on utilise la fonction input avec l'argument 's' signifiant string. La concaténation de texte s'effectue comme pour les matrices et vecteurs.
Essayez :

>> txt2 = input('Tapez votre texte','s')
>> txt3 = [ txt2; reverse(txt2) ]

L'affichage du texte est possible par les commandes disp et sprintf.

disp permet d'afficher une variable ou une chaîne de caractère, ou toute combinaison licite des 2. Le mélange de variables numériques et de caractères se fait grace à la fonction num2str qui convertit un nombre en chaîne (littéralement : number to string). Il arrive cependant qu'une variable numérique soit sur plusieurs lignes, comme c'est le cas pour les matrices. Aussi, la fonction strvcat permet de mettre en forme des variables de texte n'ayant pas le même nombre de lignes ou de colonnes.
Les différents exemples proposés ci-dessous montrent les différents cas possibles ou non:
```
>> disp(a);
>> disp(pi);
>> disp('du texte, blabla');   
>> disp('du texte'),disp('blabla')
>> disp( [ 'l''élément a(3,3) vaut : ' num2str(a(3,3)) ] ) 
>> disp( [ 'La matrice A vaut :' num2str(a) ] )
>> disp( strvcat('La matrice A vaut :', num2str(a)) ) 
>> disp('La matrice A vaut : '), disp(a)
```
sprintf est la fonction similaire à la fonction printf du langage C. Par rapport à la fonction disp, elle permet d'inclure plus facilement des résultats numériques au milieu de texte, et de choisir la précision d'affichage.
Regardez l'aide de cette fonction et commentez les différents exemples suivant :
```
>> sprintf('%.25f',pi)
>> sprintf('%.3f',pi);
>> disp(sprintf('%.3f',pi));
>> sprintf('%d  ',a) 
>> sprintf('A est une \nmatrice %dx%d',size(a,1),size(a,2))
```

Graphiques 2D

Un graphique sert à représenter dans une grande majorité des cas une grandeur physique. Il est donc primordial de gérer les unités des axes que l'on utilise. De nombreuses fonctions servent à personnaliser les axes en ajoutant vos propres labels, légendes et titres. Différents types de représentations sont aussi possibles, suivant le type de données que l'on désire représenter. Nous ne présentons ici que les graphiques de type courbes, mais il existe aussi des fonctions réalisant des histogrammes, des barres ou des camenberts pour les données de types statistiques ou proportionnelles (help specgraph pour plus de détails).

Les représentations se font en coordonnées cartésiennes mais aussi polaires ou cylindriques. Les principales fonctions d'affichage sont :

plot relie deux points successifs par une ligne, ce qui donne une courbe.
stem les différents points ne sont pas reliés entre eux, mais apparaissent comme des échantillons.
stair les valeurs des points restent identiques jusqu'au point suivant. Similaire à un bloqueur d'ordre 0 pour un échantillonneur (capacité très grande).
comet trace la courbe de manière continue, comme une comète qui passe.
semilogx, semilogy, loglog idem que plot sur une courbe, semi logarithmique en x ou y ou sur une courbe logarithmique.

La première utilisation d'une de ces fonctions entraîne la création d'une fenêtre appelée figure. Les suivantes se tracent par défaut dans la même figure, en effaçant la courbe précédente. Il est donc nécessaire de créer une nouvelle figure pour afficher 2 graphiques différents. La commande figure crée une nouvelle fenêtre et la commande close ferme la fenêtre en cours d'utilisation. Toute les figures sont repérées par un numéro qui peut être utilisé comme argument de figure ou close pour rappeler une ancienne figure.

La syntaxe est la même pour toutes ces fonctions. Elle permet notamment de tracer plusieurs courbes en même temps : plot(x1,y1,'couleur1',x2,y2,'couleur2',... ). L'argument couleur est 1 caractère, correspondant à une couleur dont la liste est donnée dans l'aide de la fonction plot. Quand on ne désire tracer qu'une seule courbe, les arguments x1 et 'couleur' sont optionnels. Attention, car on perd dans ce cas là l'information sur l'axe des abscisses, et donc sur une unité (souvent le temps ou la fréquence) de la grandeur représentée.

Il est aussi possible de superposer les courbes à l'aide de la commande hold on, qui maintient l'affichage. De la même manière hold off supprime le maintient de l'affichage. Ainsi :

>> x = 0:0.1:2*pi;
>> y1 = sin(x);   
>> y2 = cos(x);
>> plot(x,y1,'r',x,y2,'b')

Équivaut à

>> plot(x,y1,'r')
>> hold on;
>> plot(x,y2)

Créez un fichier ``.m'' permettant de comparer les différents types de visualisations sur le signal sinusoïdal généré précédemment.

La fonction polar permet de représenter des fonctions en coordonnées polaires. Ceci présente un grand intérêt pour les diagrammes de directivité. Par exemple, ici un diagramme de directivité de type cardioïde.

>> theta = 0:.1:2*pi;
>> r = 1 + cos(theta);
>> polar(theta,r)

Rq : il peut être nécessaire de faire un hold off avant !

Gestion des axes

Les différentes fonctions suivantes permettent de gérer les labels des axes et commentaires sur les figures, ainsi que diverses fonctions pour manipuler les graphiques.

title : title('Texte du titre') Ajoute un titre à la figure.
xlabel : xlabel('Unité des x')
ylabel : ylabel('Unité des y')
legend : legend('Nom de la courbe 1','nom courbe 2', ...)
grid : grid on, grid off, quadrille ou non le graphique.
zoom : permet de zoomer dans la figure a l'aide de la souris (clic gauche = zoom +, clic droite = zoom -, double clic droite = retour à l'affichage de départ, bouton gauche appuyé $\rightarrow$ dessin de la zone à zoomer).
clf : efface la figure en cours d'utilisation.
ginput : ginput(n) récupère les coordonnées de n points cliqués à la souris dans la figure en cours.

Images et graphiques 3D

Les fonctions de représentation en 3D s'utilisent de la même manière que les fonctions 2D. La seule différence vient de la taille des données à représenter. Typiquement, on va représenter en 3D des données contenues dans une matrice, en considérant par exemple les lignes et les colonnes comme un quadrillage de l'espace, et les valeurs en chaque point de la matrice représentent une amplitude (pression, tension, ...).

Il est alors possible de représenter les amplitudes soit sous forme d'une image ou chaque couleur représente une valeur d'amplitude soit sous forme d'un graphique en 3 dimensions où en plus de la couleur, l'axe des z (hauteur) représente l'amplitude. Les principales fonctions d'affichage 3D sont :

surf : surf(x,y,z), courbe 3D où x et y sont les axes et z la matrice des amplitudes
mesh : mesh(x,y,z). Idem que surf
image, imagesc : imagesc(x,y,z). Visualisation d'une image, les couleurs sont proportionnelles aux amplitudes.
shading : shading interp améliore le rendu d'une courbe 3D, en la lissant.
colormap : colormap(cool) différentes plages de couleur.
view : view(azimut,elevation) permet de régler l'angle de vue de la courbe (azimut, rotation par rapport à un axe vertical, elevation par rapport à un axe horizontal )
rotate : Permet de faire tourner la figure à l'aide de la souris

Par exemple, pour représenter le mode (1,1) de vibration d'une plaque, on génère la matrice

, et

>> y = 0:0.1:pi;        
>> x = 0:0.1:pi;  
>> n = 1; m = 1;
>> z = sin(n*x)'*sin(m*y);  
>> figure(1); clf;
>> surf(x,y,z);
>> shading interp
>> figure(2), clf, imagesc(x,y,z)

Division d'une figure en sous-figures

La commande subplot permet de séparer une figure en une matrice de sous-figures. Elle s'utilise avant une commande de dessin pour signifier que la courbe devra être dessinée dans une sous-figure.

La syntaxe est subplot(n_ligne,n_col,num_fig) et la figure est séparée en n_lignes * n_col sous figures, réparties sur n_lignes lignes et n_col colonnes. num_fig correspond au numéro de la sous figure dans laquelle on désire tracer la courbe, les sous-figures étant numérotées de gauche à droite puis de haut en bas.

>> subplot(2,2,2), plot(x,sin(x))
>> subplot(2,2,3), plot(x,sin(x))

À titre d'exercice, réaliser un script permettant de voir en 3D les modes (1,1), (1,2), (1,3), (2,2), (3,2) et (3,3) de la plaque définie ci-dessus dans une même figure.

Les fonctions

Les fonctions sont le deuxième type de fichiers ``.m''. Comme les scripts, il s'agit de fichiers texte, mais elles implémentent une fonction, de manière interne au fichier. Ainsi, on lui passe des paramètres d'entrée et la fonction rend des résultats. Les variables utilisées dans les fonctions sont invisibles depuis l'espace de travail. Seuls les résultats seront visibles.

Un fichier fonction débute par le mot function, suivi du nom de la fonction, et des paramètres d'entrée sortie. La déclaration est de la forme :

function [ resultat1, resultat2, ... ] = mafonction(paramètre1,paramètre2,... )

   % Les commentaires situés juste après la déclaration de la fonction 
   % constituent l'aide obtenue par la commande 
   % >> help mafonction

Le nom du fichier .m et de la fonction doivent impérativement être identiques. Dans l'exemple ci-dessus, le fichier doit s'appeler mafonction.m. Elle sera appelé depuis Matlab, un script ou une fonction de la manière suivante :

>> [ y, z ] = mafonction(a,b)

Un des avantages de Maltab est qu'il est possible de récupérer les sources de tous les fichiers ``.m'' par la commande type nom_fonction. Vous pouvez ainsi vous inspirer de tous les programmes déjà existants pour créer vos propres fonctions. Par exemple, regardez la source de la fonction moyenne (mean). Notez au passage l'importance des commentaires et de l'aide par rapport au programme lui-même.

>> type mean

Exemple

Créez une fonction calculant la valeur efficace d'un vecteur. Cette fonction a comme paramètre d'entrée un vecteur et renvoie comme résultat la valeur efficace, calculée par la formule :

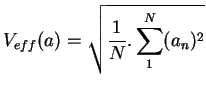$\displaystyle V_{eff}(a) = \sqrt{\frac{1}{N} . \sum_1^N (a_n)^2 }$ où $\displaystyle N$ est le nombre de points du vecteur a. $\displaystyle$

Commentez votre fonction et créez une aide sur votre fonction.
Testez la sur un vecteur sinusoïdal.

Application

Créez une fonction TraceBode( $\omega,H(\omega)$ ) effectuant le diagramme de Bode d'un système, ayant comme paramètres d'entrées le vecteur des fréquences utilisées et la fonction de transfert (complexe) calculée aux fréquences correspondantes. Il n'y a pas de paramètres de sortie mais la fonction affichera dans une figure d'une part le module en dB de la fonction de transfert du système et d'autre part la phase du système. Les abscisses seront graduées en Hertz et les ordonnées en dB. Les graphiques seront semi logarithmiques.
Écrivez un fichier script traçant le diagramme de Bode de filtres Passe Haut et Passe Bas du premier ordre. Les fonctions de transfert de ces 2 filtres sont :

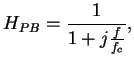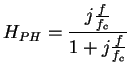$\displaystyle H_{PB} = \frac{1}{1+j \frac{f}{f_c}} ,$ et $\displaystyle H_{PH} = \frac{j \frac{f}{f_c}}{1+j\frac{f}{f_c}}$ (1.3)
La fréquence de coupure sera demandée à l'utilisateur
L'affichage sera effectué par appel de la fonction TraceBode créée précédemment.

Next: TP 2 : Programmation Up: Previous: Contents Contents

GONON Gilles 2001-10-02