


Next: TP 3 : Notions
Up:
Previous: TP 1 : Prise
Contents
Subsections
Ce TP illustre et propose de mettre en 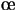 uvre les principales
syntaxes de programmation algorithmiques utilisables sous Matlab.
Ce TP présente aussi les opérateurs relationnels permettant
d'effectuer des tests conditionnels. Les structures conditionnelles et
itératives sont présentées par l'intermédiaire d'algorithmes simples
vus en TD.
uvre les principales
syntaxes de programmation algorithmiques utilisables sous Matlab.
Ce TP présente aussi les opérateurs relationnels permettant
d'effectuer des tests conditionnels. Les structures conditionnelles et
itératives sont présentées par l'intermédiaire d'algorithmes simples
vus en TD.
Le compte rendu de ce TP comprendra, en plus des explications
demandées au cours du texte, les scripts d'exemples et d'applications,
commentés de manière abondante.
N'oubliez donc pas qu'un bon
programme, est un programme bien commenté !
Il existe deux structures possibles permettant de réaliser des
tests sur les données. La structure if permet de tester la
valeur d'une variable et d'effectuer différents traitement suivant les
cas testés. La structure switch permet de choisir entre
différents cas, et de faire correspondre un traitement adapté à chacun
des cas reconnus.
La structure if est indispensable à la programmation. Elle est
présente dans tous les langages, mais utilise des syntaxes un peu
différentes.
En langage Matlab, elle est déclarée de la manière suivante
Seul le if ...end est obligatoire. else et elseif sont
facultatifs et permettent d'effectuer des tests supplémentaires.
Le script suivant vous donne un exemple d'utilisation de la fonction
if sous Matlab.
Tapez le et testez les différents cas possibles. Modifiez le ensuite
pour qu'il indique en plus si le nombre est compris entre 100 et 200.
% Exemple d'utilisation de if, elseif, ... end
nb = input('Rentrez un nombre : ');
if (nb < 100)
disp('votre nombre est < 100')
elseif (nb == 100)
disp('votre nombre est 100')
else
disp('votre nombre est > 100')
end
Lorqu'un test est effectué en bloc sur un vecteur, il suffit qu'une
valeur ne vérifie pas le test pour que la condition ne soit pas
vérifiée. Essayez et commentez l'exemple ci-dessous
>> a = zeros(1,10);
>> if a == 0, a(5) = 1, end
???
>> if a == 0, a(5) = 0, end
???
La deuxième structure permet le choix entre différents cas. Le seul
test effectué dans cette structure est donc un test d'égalité. Cette
structure est déclarée par
Le test d'égalité est donc effectué par la fonction par rapport à
chaque cas (case). otherwise est une alternative lorsque
la variable testée n'a pas d'égal parmi les différents cas.
Le script suivant vous donne un exemple d'utilisation de la fonction
switch sous Matlab.
Tapez le et testez les différents cas possibles. Modifiez le pour
qu'il indique ``c'est le week end '' si le jour est samedi ou
dimanche et qu'il indique ``ca n'est pas un jour de la semaine ''
si la chaîne rentrée par l'utilisateur ne correspond pas à un jour de
la semaine.
% Un exemple d'utilisation de switch
jour = input('Quel jour sommes nous ? ','s');
switch jour
case 'lundi'
jr = 5;
case 'mardi'
jr = 4;
case 'mercredi'
jr = 3;
case 'jeudi'
jr = 2;
case 'vendredi'
jr = 1;
otherwise
jr = 0;
end
disp([ 'Encore ' num2str(jr) ' jours avant le weekend' ])
Écrivez un script permettant d'effectuer la conversion
de Franc vers Euro ou de Euro vers Franc, à partir de l'algorithme
effectué en TD.
Dans un premier temps, le sens de conversion est choisi
par l'utilisateur, avant qu'il rentre le montant (en 2 questions).
Gardez votre programme, il vous sera utile dans la troisième
partie de ce TP.
Afin d'illustrer l'utilisation du choix par cas, on se propose de réaliser
un petit programme permettant à l'utilisateur de choisir visualiser
différents diagrammes de directivité. Les directivités seront affichés
sur des diagrammes polaires, en représentant l'amplitude 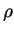 pour un
angle
pour un
angle 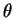 variant de 0 à
variant de 0 à 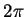 .
.
Voici un petit rappel des différentes courbes de directivité de
microphones à gradient de pression du premier et second ordre.
- Un microphone à gradient de pression du
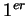 ordre est
constitué de 2 microphones à pression pour permettre la mesure d'un
gradient entre les 2 capsules. La tension délivrée est en première
approximation une combinaison linéaire des pressions captées par les
2 microphones. Ceci conduit pour les courbes de directivité à
l'équation :
ordre est
constitué de 2 microphones à pression pour permettre la mesure d'un
gradient entre les 2 capsules. La tension délivrée est en première
approximation une combinaison linéaire des pressions captées par les
2 microphones. Ceci conduit pour les courbes de directivité à
l'équation :
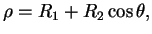 où où 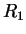 et et 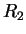 sont des constantes indépendantes de sont des constantes indépendantes de 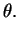 |
(2.1) |
Les courbes de directivité vont donc varier en fonction des constantes
des 2 microphones à pression. Notamment :
- Omnidirectionnel : Si
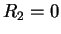 , c'est le cas du microphone à
pression et
, c'est le cas du microphone à
pression et
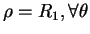 ,
,
- Bidirectionnel : Si
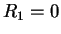 , c'est le cas du microphone à
vitesse et
, c'est le cas du microphone à
vitesse et
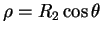 ,
,
- Cardioïde : Pour
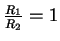 , on obtient
, on obtient
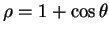 . Cette courbe est aussi appelée courbe
unidirectionnelle, et elle est très recherchée car elle permet entre
autre de supprimer une source génante en l'orientant vers le zéro de la courbe.
. Cette courbe est aussi appelée courbe
unidirectionnelle, et elle est très recherchée car elle permet entre
autre de supprimer une source génante en l'orientant vers le zéro de la courbe.
- Supercardioïde : Pour
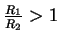 , souvent
, souvent
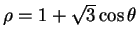 ,
,
- Hypercardioïde : Pour
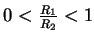 , souvent
, souvent
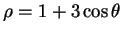 .
.
- Un microphone à gradient de pression du second ordre est
constitué de 2 microphones à gradient de pression du
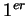 ordre
identiques. La courbe de directivité pour ce type de microphone
s'écrit alors :
ordre
identiques. La courbe de directivité pour ce type de microphone
s'écrit alors :
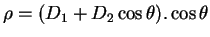 |
(2.2) |
Les courbes de directivité sont nommées de la même façon que pour les
micros du 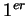 ordre, mais elles ont des allures différentes,
souvent plus sélective. On retrouve donc par exemple :
ordre, mais elles ont des allures différentes,
souvent plus sélective. On retrouve donc par exemple :
- Bidirectionnel :
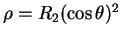 ,
,
- Cardioïde :
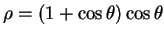 .
.
Le script proposera à l'utilisateur soit de voir un diagramme au choix
parmi les diagrammes présentés, ou toute autre combinaison, soit de
comparer pour un type de diagramme les ordres 1 et 2.
On prendra soin de bien nommer les diagrammes, en leur donnant un
titre et en proposant des unités pour les axes.
Il existe deux grands types de boucles : les boucles de type for
dont on connait le nombre d'itérations et les boucles de type while dont le nombre d'itérations peut évoluer à l'interieur de la
boucle.
La structure for se présente comme suit :
Cette structure est à éviter autant que possible sous Matlab car
elle est très coûteuse en temps de calcul par rapport au calcul
matriciel. Dans de nombreux cas, il est possible d'utiliser de faire
vos traitements en blocs, par des opérations sur les matrices, et il
n'est pas nécessaires d'utilliser de boucles for.
Les principaux cas où il est nécessaire d'utiliser ces boucles sont :
- La génération de suites récurrentes, dans lesquelles il est
nécessaire de connaître un ou plusieurs termes pour calculer le
terme suivant.
- Le traitement répétitif de données de longueurs différentes qui
ne peuvent donc pas être rangées sous forme matricielle.
- La demande à l'utilisateur d'un nombre connu de valeurs
nécessaires pour la suite du programme.
L'utilisation des fonctions tic et toc entre une série de
commandes permet de voir le temps mis pour effectuer ces
commandes. Ceci permet par exemple de comparer l'efficacité en temps
de deux algorithmes différents réalisant la même fonction.
L'exemple suivant compare donc le temps mis pour la création d'un
vecteur de 1000 points, avec et sans boucle for.
% Un exemple de boucle for
tic
vect = [];
for k = 1:1000
vect(k) = log(k);
end
toc
% Ceci et équivalent à :
tic
k = (1:1000);
vect = log(k);
toc
Créez un script demandant successivement à l'utilisateur 5 valeurs qui
seront rangées dans une variable de type vecteur appelée valeurs. Elle seront demandées lors d'une boucle for, à
chaque itération :
- $&bull#bullet;$
- Rentrez la valeur 1
- $&bull#bullet;$
- Rentrez la valeur 2
- $&bull#bullet;$
- Rentrez la valeur 3
- &vellip#vdots;
Une fois rentrées, ces valeurs seront affichées dans l'ordre croissant.
Le tri des valeurs d'un vecteur est effectué grace à la fonction sort, dont vous regarderez l'aide.
La structure while se présente comme suit :
La boucle continue donc ``tant que '' le test renvoie une valeur de
1. Ce test est aussi appelé condition d'arrêt. La variable de
test doit donc être actualisée pendant l'exécution de la boucle afin
que celle-ci s'arrête. Elle doit aussi être initialisée avant la
première exécution de sorte que le test renvoie 1, et que la boucle
soit effectuée au moins une fois. Il peut aussi arriver volontairement
dans le déroulement d'un programme qu'une boucle while ne soit jamais
exécutée.
Essayez l'exemple suivant. Modifez le pour que la question posée
soit ``voulez vous continuer ? '' et qu'une réponse autre que `` oui '' ou ``non '' entraîne la remarque ``je ne comprends pas la
réponse '' avant de recommencer la boucle.
% Un exemple de boucle while
% (nombre d'itérations inconnu)
% initialisation de la variable du test
reponse = 'cekonveutmaipawi';
while(strcmp('oui',reponse)~=1)
reponse = input('voulez vous arrêtez ? ','s');
end
Modifiez le jeu de pile ou face pour qu'il se fasse en trois manches
gagnantes entre l'utilisateur et l'ordinateur. Le score sera affiché
après chaque coup.
Les opérateurs relationnels sont utilisés pour effectuer les
différents tests nécessaires dans les boucles et structures
conditionnelles (help relop. On distingue les opérateurs
logiques des opérateurs arithmétiques.
- Opérateurs logiques : Ce sont les fonctions OU(OR), notée ``
|'',
ET(AND), notée ``&'', COMPLÉMENT(NOT), notée ``~'' et
OU EXCLUSIF(XOR), notée ``xor(a,b)'', qui considèrent tous les
nombres comme binaires, prenant la valeur 0 pour les nombres nuls
et la valeur 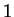 pour tous les autres. La comparaison est
possible entre des matrices de même taille ou par rapport à un
scalaire.
pour tous les autres. La comparaison est
possible entre des matrices de même taille ou par rapport à un
scalaire.
Essayez et expliquez les test suivants :
>> ~(-3:4)
>> xor(~(-1:1),(-1:1))
>> (eye(3) & 1)
>> (eye(3) | 0)
- Opérateurs arithmétiques : Ce sont les 6 fonctions de comparaisons
entre les nombres :
- supériorité
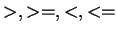 ,
,
- égalité
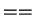 et différence
et différence 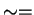 .
.
Les tests s'effectuent par rapport aux valeurs des
nombres mais le résultat à ces tests prends la valeur 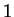 quand le
test est vrai et la valeur 0 quand il est faut. La comparaison est
possible entre des matrices de même taille ou par rapport à un
scalaire.
quand le
test est vrai et la valeur 0 quand il est faut. La comparaison est
possible entre des matrices de même taille ou par rapport à un
scalaire.
Essayez et expliquez les test suivants :
>> (eye(3) == 0)
>> B = (eye(3) ~=1)
>> (1:10) > 3.5
>> (1:10) <= 5
>> sqrt(0:.2:2) <= (0:.2:2).^2
>> (1:10)>4 & (1:10)<=6
Une fonction très utile de Matlab pour le traitement en bloc des
données, c'est-à-dire sans faire de boucle for, est la
fonction find qui permet, en plus d'effectuer un test sur une
matrice ou un vecteur, de récuperer les indices correspondant aux
éléments vérifiant le test. Cette fonction permet alors de traiter en bloc tous
les indices de la matrice vérifiant le test, en évitant souvent une
boucle for.
Testez et commentez les exemples suivants :
>> a = (1:10);
>> indices = find(a > 3.5)
>> a(indices) = -a(indices)
>> B = eye(3);
>> B(find(B == 0)) = 2
Cette fonction permet aussi de travailler sur les chaînes de caractères,
pour repérer par exemple un caractère spécial ou attendu. Les
fonctions utiles à cette fin sont :
- lower(chaîne) qui permet de passer une chaîne
contenant des caractères en majscules en minuscules. La distinction
entre majuscule et miniscule est ainsi supprimée.
>> lower('BlaBLA')
>> chaine = 'BonJouR Les DEUST';
>> indices = find(lower(chaine) == 'l')
>> disp(chaine(1:indices-1))
- str2num(chaîne) convertit une chaîne de caractère
représentant un nombre en ce nombre. Il faut en effet bien dissocié
les chaîne de caractères et ce qu'elle représente. Une chaîne de
caractères est codée par la valeur ASCII des caractères, c'est à
dire des entiers entre 0 et 255. Par exemple :
>> chaine = '1024'
>> chaine + 10 % Ceci ajoute 10 à la valeur ASCII de chaque caractère
>> char(chaine + 10) % Affiche les valeurs ASCII en caractères
>> b = str2num(chaine) + 10
En vous inspirant des exemples ci-dessus, modifier le programme de
conversion Franc
 Euro pour rentrer le montant et
l'unité en une fois, sous forme de chaîne de caractères. Séparer le
le montant et les unités, pour convertir le montant en chiffre et
effectuer les opérations demandées.
Euro pour rentrer le montant et
l'unité en une fois, sous forme de chaîne de caractères. Séparer le
le montant et les unités, pour convertir le montant en chiffre et
effectuer les opérations demandées.
Créez un script permettant à l'utilisateur d'entrer successivement 3 valeurs de
fréquences et d'amplitudes pour des sinus. Générez alors une matrice
de taille 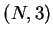 dont chaque colonne contient un sinus répondant
aux caractéristiques rentrées précédemment.
dont chaque colonne contient un sinus répondant
aux caractéristiques rentrées précédemment. 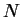 est le nombre de
points temporels, fixé dans le script à 256.
est le nombre de
points temporels, fixé dans le script à 256.
On désire alors écrêter chacun de ces sinus par rapport à un seuil
demandé à l'utilisateur (entre 0 et l'amplitude maximale). Cela
revient à chercher les valeurs du signal situées en dehors de
l'intervalle
![$ [-seuil,+seuil]$](img82.gif) et à les fixer à
et à les fixer à 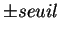 .
.
Afficher dans une première figure, sur deux sous-figures, les signaux
originaux et les signaux écrêtés.
Afficher enfin dans une deuxième figure,
sur le même axe, la somme des 3 trois signaux originaux et la somme
des 3 signaux écrêtés.
La somme des 3 signaux écrêtés est-elle égale à la somme écrêtée des 3
signaux originaux ?
Conclure sur la linéarité de l'opération d'écrêtage, présente dans
de nombreux appareils ou composants électroniques (transistor, ampli opérationnel,
...).



Next: TP 3 : Notions
Up:
Previous: TP 1 : Prise
Contents
GONON Gilles
2001-10-02
![]() uvre les principales
syntaxes de programmation algorithmiques utilisables sous Matlab.
Ce TP présente aussi les opérateurs relationnels permettant
d'effectuer des tests conditionnels. Les structures conditionnelles et
itératives sont présentées par l'intermédiaire d'algorithmes simples
vus en TD.
uvre les principales
syntaxes de programmation algorithmiques utilisables sous Matlab.
Ce TP présente aussi les opérateurs relationnels permettant
d'effectuer des tests conditionnels. Les structures conditionnelles et
itératives sont présentées par l'intermédiaire d'algorithmes simples
vus en TD.




![]() dont chaque colonne contient un sinus répondant
aux caractéristiques rentrées précédemment.
dont chaque colonne contient un sinus répondant
aux caractéristiques rentrées précédemment. ![]() est le nombre de
points temporels, fixé dans le script à 256.
est le nombre de
points temporels, fixé dans le script à 256.
![]() et à les fixer à
et à les fixer à ![]() .
.