


Next:TP
5 : RécupérationUp: Previous:TP
3 : NotionsContents
Subsections
TP 4 : Filtrage et Analyse spectrale
Les programmes nécessaires pour ce TP sont disponibles à
l'adresse :
http://www.univ-lemans.fr/~s973476/filtres/filtres.zip
Filtrage numérique
Création des filtres
Le filtrage est une opération inhérente à tout système
physique. Le passage au numérique ne se fait toutefois pas sans
quelques problèmes d'échantillonnage car la numérisation
des filtres se fait souvent avec une perte des propriétés
des filtres. C'est pourquoi il existe de nombreuses méthodes de
conception de filtres numériques. Nous n'allons pas voir ici ces
techniques en détails mais juste en utiliser une: la méthode
de Remez qui permet d'obtenir la réponse impulsionnelle de filtres
de longueur finie.
La méthode de Remez voit le problème de synthèse
d'un filtre comme un problème d'approximation d'une fonction contenue
dans le gabarit par un pôlynome. Cette méthode est la plus
utilisée en synthèse de filtres RIF car elle fait partie
du domaine public et est souvent intégrée dans les logiciels
de traitement du signal.
Définition d'un filtre
un filtre est défini par son gabarit. Le gabarit d'un filtre est
constitué des limites de tolérance pour les différentes
éléments du filtre, à savoir :
-
La fréquence de coupure,
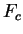 ,
,
-
L'atténuation dans la bande coupée, en dB,
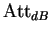 ,
,
-
L'ondulation dans la bande passante, en dB,
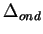 ,
,
-
La largeur de la bande de transition, située entre la fréquence
de coupure et la zone atténuée, car la coupure d'un filtre
n'est jamais parfait,
 .
.
Il peut y avoir plusieurs fréquences de coupures dans le cas de
filtres autres que passe-haut ou passe-bas. La figure ci-dessous illustre
les différentes notations de gabarit suivant les filtres.
 Les fonctions passebas, passehaut et passebande génèrent
la réponse impulsionnelle des filtres, par la méthode de
Remez, correspondant à un gabarit qui vous sera demandé.
L'ordre du filtre correspond à la longeur de la RI moins 1. Il est
proportionnel à la complexité du filtre.
Les fonctions passebas, passehaut et passebande génèrent
la réponse impulsionnelle des filtres, par la méthode de
Remez, correspondant à un gabarit qui vous sera demandé.
L'ordre du filtre correspond à la longeur de la RI moins 1. Il est
proportionnel à la complexité du filtre.
Il est important de distinguer la réponse impulsionnelle
d'un filtre, sa réalisation temporelle, qui sert à l'opération
de filtrage par convolution, du gabarit, qui indique les limites
fréquentielles que doit respecter le filtre. La réponse
fréquentielle du filtre, obtenue par transformée de Fourier
de sa RI, doit donc être contenue dans le gabarit pour que le filtre
soit utilisable à bon essient. Il arrive aussi qu'un filtre ne rentre
pas dans le gabarit désiré, si la méthode diverge.
Il faut donc vérifier les réponses fréquentielles
de vos filtres après utilisation des fonctions
passebas, passehaut
et passebande.
Utilisation des filtres
L'opération de filtrage est réalisée par convolution
de la RI du filtre avec le signal que l'on veut filtrer. En numérique
la convolution induit un décalage de l'ordre du filtre. Il correspond
en analogique au temps de réponse du filtre.
La convolution correspond à une multiplication du spectre du
signal par celui du filtre, ou encore en dB, après passage au logarithme
à la addition de la réponse fréquentielle au spectre
du signal. En effet
Signal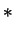 Filtre
Filtre |
(4.1) |
La convolution est réalisée sous Matlab par la fonction
conv.
À titre d'exemple :
-
Pour une fréquence d'échantillonnage de 8kHz, créez
un filtre passe bas de fréquence de coupure
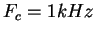 de largeur de bande de transition
de largeur de bande de transition 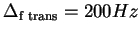 ,
ayant une ondulation dans la bande passante
,
ayant une ondulation dans la bande passante 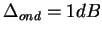 et une atténuation dans la bande coupée
et une atténuation dans la bande coupée 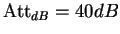 .
.
-
Dessinez le gabarit.
-
Visualisez la réponse impulsionnelle du filtre et assurez vous que
sa réponse fréquentielle est bien dans le gabarit.
-
Filtrer deux signaux sinusoïdaux de fréquences respectives
inférieure et supérieure à
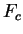 .
Quel est l'effet du filtre sur ces signaux ?
.
Quel est l'effet du filtre sur ces signaux ?
-
Mesurez sur l'allure temporelle des signaux filtrés le décalage
induit par le filtre numérique. Comparez ce décalage par
rapport à la longueur du filtre utilisé. Le décalage
varie-t-il pour les 2 fréquences, est-ce qu'il y a un déphasage
comme pour un filtre RC du premier ordre ?
-
Quelle partie utile du signal filtré de même longueur
que le signal original peut-on garder ?
Application au filtrage d'harmoniques
La distortion harmonique est une forme de distortion courante en musique.
Elle consiste à ajouter des harmoniques - des fréquences
multiples de la fréquence fondamentale - au signal de départ.
-
Ajoutez à un signal sinusoïdal pur ses 5 premières harmoniques
impaires, de même amplitude.
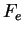 étant fixé à
étant fixé à 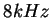 ,
choisissez une valeur de
,
choisissez une valeur de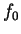 adéquate. Visualiser la forme d'onde et le spectre du signal.
adéquate. Visualiser la forme d'onde et le spectre du signal.
-
Réalisez les filtres adéquats pour extraire les composantes
correspondant à :
-
La fréquence fondamentale (harmonique 1),
-
L'harmonique 5,
-
L'harmonique 11.
Les filtres seront réalisés à l'aide des fonctions
passebas,passebande
et passehaut, basées sur la méthode de remez.
-
Réalisez le filtrage à l'aide de la fonction conv.
-
Visualisez les signaux filtrés et leur spectre.
-
Notez les amplitudes des signaux filtrés, et interprétez
leurs valeurs.
Application à la réduction
de bruit
Le filtrage sert aussi à des applications d'égalisation,
c'est-à-dire de pondération relative d'une partie du spectre
par rapport à une autre. Typiquement, le réglage tone
d'une chaîne Hi-Fi est un filtre passe bande dont on fait varier
la fréquence centrale.
Ici, on veut rehausser une composante sinusoïdale noyée
dans le bruit. Un bruit blanc à un spectre étalé sur
toute la bande fréquentielle tandis qu'un sinus à un spectre
très concentré.
-
Générez une sinusoïde de fréquence 1000 Hz échantillonnée
à 10kHz.
-
Ajoutez du bruit au signal précédent de manière à
obtenir un RSB de 10 dB.
-
Comment doit-on choisir le gabarit du filtre pour atténuer le bruit
?
-
Réalisez le filtrage et comparez les spectres et allures temporelles
du signal bruité et du signal débruité.
Analyse spectrale par TFD
On désire voir ici différents effets de la TFD en terme de
précision d'analyse et de résolution fréquentielle.
Un algorithme de transformée de Fourier rapide est réalisé
par la fonction fft. Cet algorithme est particulièrement
rapide lorsque la taille des signaux analysés est une puissance
de 2 (64, 128, 256, 512, 1024, 2048, ...). On prendra donc soin de travailler
sur des signaux dont la longueur est une puissance de 2.
Influence de la taille de la
fenêtre d'observation
Il est possible d'appliquer la TFD sur la globalité ou sur une partie
d'un signal de longueur 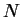 .
La partie analysée est appelée fenêtre d'observation.
Pour un même signal sinusoïdal échantillonné à
1kHz de fréquence 100 Hz et de longueur 512 points, on va observer
le module de la FFT (sans le logarithme) sur des fenêtres dont la
longueur varie. Le résultat à mettre en évidence est
que la précision fréquentielle augmente avec la taille la
fenêtre.
.
La partie analysée est appelée fenêtre d'observation.
Pour un même signal sinusoïdal échantillonné à
1kHz de fréquence 100 Hz et de longueur 512 points, on va observer
le module de la FFT (sans le logarithme) sur des fenêtres dont la
longueur varie. Le résultat à mettre en évidence est
que la précision fréquentielle augmente avec la taille la
fenêtre.
-
Pour des tailles de fenêtres de 16,128 et 256 points, donnez à
chaque fois la largeur du lobe principal.
-
Vérifiez que le produit de la largeur du lobe principal par la durée
d'observation est constant.
Fenêtre d'analyse
Une fenêtre d'analyse est une enveloppe que l'on donne au signal
avant de l'analyser par TFD. Leur but est de réduire les lobes secondaires
pour que le spectre observé tende vers le résultat théorique
qui est pour une sinusoïde une raie pure à la fréquence.
Les analyseurs de spectre propose de nombreuses fenêtres d'analyse,
qui ont chacune de effets différents (Hanning, Hamming, Blackman,...).
Observez l'influence du fenêtrage sur l'allure du spectre, notamment
au niveau des lobes secondaires et de la largeur du lobe principal. Pour
cela comparer sur les spectres en dB les effets d'une fenêtre
de Hanning et d'une fenêtre de Blackman. Ces deux fenêtres
sont réalisées par les fonctions hanning et blackman
et le fenêtrage est réalisé en multipliant les formes
de fenêtres terme à terme avec le signal.
Résolution Fréquentielle
de la TFD
La résolution fréquentielle de la TFD d'un signal est définie
par le nombre de points d'analyse 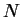 et la fréquence d'échantillonnage du signal
et la fréquence d'échantillonnage du signal 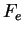 par la formule :
par la formule :
Résolution Fréquentielle 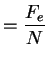 |
(4.2) |
On veut voir ici les limites de l'analyse au niveau de la détection
de sinusoïdes proches. Cette notion est importante lors de l'analyse
de vibrations de systèmes mécaniques ayant des modes proches.
-
Générez un signal échantillonné à 1kHz
de 1024 points, constitué de 2 sinusoïdes d'amplitudes égales
et de fréquences respectives 100 Hz et 105 Hz.
-
Déterminez expérimentalement la durée d'observation
en dessous de laquelle on ne peut plus séparer les lobes principaux
des deux composantes.
-
Que vaut la longueur théorique
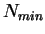 qui ne permet pas de séparer ces 2 raies ?
qui ne permet pas de séparer ces 2 raies ?
-
Obtient-on un meilleur résultat en doublant simultanément
la fréquence d'échantillonnage et la taille de la TFD ?
-
Quel serait le choix le plus économique en terme de longueur de
signaux et de fréquence d'échantillonnage pour effectuer
une mesure d'une plaque vibrante sur la zone de fréquence
![$ [0,500Hz]$](img138.gif) et qui aurait des modes à
et qui aurait des modes à 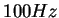 et
et 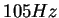 que l'on souhaite distinguer ?
que l'on souhaite distinguer ?



Next:TP
5 : RécupérationUp: Previous:TP
3 : NotionsContents
GONON Gilles 2001-10-02
