axe_temps = (0:N-1)/Fe;
axe_freq = (0:N-1)*Fe/N;
Ce TP a pour but de présenter les notions simples de traitement numérique du signal en terme d'échantillonnage et d'analyse spectrale, au travers de la transformée de Fourier discrète et des problèmes de repliement de spectre.
Un signal numérique est défini par un nombre d'échantillons N relevés à une fréquence d'échantillonnage Fe. Les signaux sont toujours captés de manière temporelle, mais on s'intéresse souvent à leur allure fréquentielle.
Afin de rester cohérents avec les mesures, il est important de respecter les grandeurs physiques impliquées dans le signal. Il faut donc définir les axes temporels et fréquentiels relatifs au signal.
Ainsi. les axes seront définis comme suit:
axe_temps = (0:N-1)/Fe;
axe_freq = (0:N-1)*Fe/N;
On désire créer 2 signaux de longueurs ![]() , échantilloné à
, échantilloné à
![]() , constitués d'une fréquence fondamentale
, constitués d'une fréquence fondamentale
![]() et des 4
premières harmoniques respectivement paires (
et des 4
premières harmoniques respectivement paires (
![]() ) et impaires (
) et impaires (
![]() ), ayant des amplitudes différentes.
Pour cela :
), ayant des amplitudes différentes.
Pour cela :
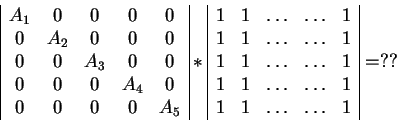 |
(3.1) |
Le rapport signal à bruit (RSB) est une quantité mesurée en dB qui donne un indice de la puissance du signal par rapport à celle du bruit. Il est mesuré par la formule :
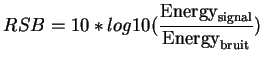 |
(3.2) |
Un ![]() positif signifie que le signal est plus énergétique que le
bruit. Pour un
positif signifie que le signal est plus énergétique que le
bruit. Pour un ![]() , il y a autant de bruit que de signal et
pour les valeurs négatives du
, il y a autant de bruit que de signal et
pour les valeurs négatives du ![]() , on dit que le signal est
dégradé.
, on dit que le signal est
dégradé.
Afin d'obtenir le spectre des signaux, on leur applique une transformée de Fourier Discrète, qui fournit une approximation du spectre du signal.
L'algorithme de FFT calcule la Transformée de Fourier Discrète des signaux de manière rapide si les séquences de signaux sont de longueurs une puissance de 2. Aussi on prendra soin de travailler sur des signaux de longueurs des puissances de 2, c'est-à-dire 64, 128, 256,..., 8192, ...
On prendra soin de tracer les spectres en dB et de graduer les abscisses en fonction de la fréquence d'échantillonnage. La conversion en dB d'un spectre se fait par
| (3.3) |
Reprenez les exemples précédents et observez les spectres des différents signaux que vous avez générés :
La modulation de fréquence (FM) est un type de modulation très utilisé en
radio pour transmettre les signaux audios par les voies
hertziennes. De manière simplifiée elle consiste à multiplier le signal
d'origine par un signal sinusoïdal à une fréquence dite porteuse
![]() .
.
Une hypothèse de la modulation en général stipule que le signal à
moduler a sa fréquence maximale
![]() , afin
d'éviter tout problème lié au repliement (pour la radio FM par
exemple la porteuse est de fréquence
, afin
d'éviter tout problème lié au repliement (pour la radio FM par
exemple la porteuse est de fréquence
![]() pour un
signal audio compris entre 0 et
pour un
signal audio compris entre 0 et ![]() ).
La démodulation est effectuée comme la modulation, en remultipliant le
signal par la fréquence porteuse.
Cela revient à faire deux translations spectrales car le
signal modulé se retrouve centré en
).
La démodulation est effectuée comme la modulation, en remultipliant le
signal par la fréquence porteuse.
Cela revient à faire deux translations spectrales car le
signal modulé se retrouve centré en ![]() et la seconde opération
ramène le signal démodulé autour de 0. Les équations ci-dessous
montrent cet effet de translation pour une sinusoïde de fréquence
et la seconde opération
ramène le signal démodulé autour de 0. Les équations ci-dessous
montrent cet effet de translation pour une sinusoïde de fréquence
![]() . Le signal modulé est constitué des fréquences :
. Le signal modulé est constitué des fréquences :
| (3.4) | |||
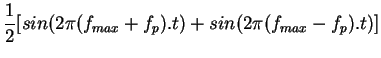 |
(3.5) |
| (3.6) | |||
| (3.7) | |||
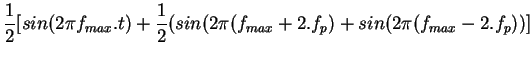 |
(3.8) |
Les signaux numériques sont conditionnés par le théorème de
Shannon, qui stipule que les fréquences qui les composent ne peuvent
en aucun cas dépasser
![]() pour les signax réels et
pour les signax réels et ![]() pour les signaux complexes.
pour les signaux complexes.
Le repliement spectral (aliasing en anglais) se manifeste lorsqu'un
signal échantillonné à la cadence
![]() -
- ![]() est la fréquence
d'échantillonnage - présente des composantes de fréquence supérieure à la fréquence
de Shannon, soit
est la fréquence
d'échantillonnage - présente des composantes de fréquence supérieure à la fréquence
de Shannon, soit
![]() .
Pour les signaux réels, toutes les
fréquences situées au dessus de
.
Pour les signaux réels, toutes les
fréquences situées au dessus de
![]() se replient,
c'est-à-dire qu'elles ne sont pas perdues mais réapparaissent dans la
zone
se replient,
c'est-à-dire qu'elles ne sont pas perdues mais réapparaissent dans la
zone
![]() .
.
L'exemple suivant a pour but de vous faire prendre conscience du phénomène de repliement.